Перенес пост сюда:
http://il2war.ru/ind...pic=784&page=43
Это специальная тема для подобных заявлений.
 Мужской
Мужской
10 Январь 2022 - 12:55
Перенес пост сюда:
http://il2war.ru/ind...pic=784&page=43
Это специальная тема для подобных заявлений.
04 Июль 2021 - 23:39
https://forum.il2stu...ols_844791_menu
Кто будет, не сочтите за труд - отстреляйте прощальный салют.
21 Май 2021 - 01:42
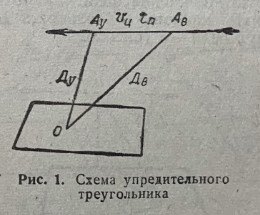
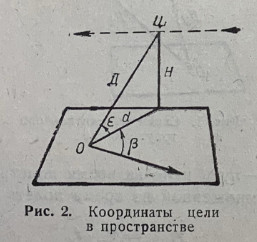
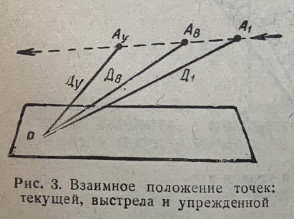
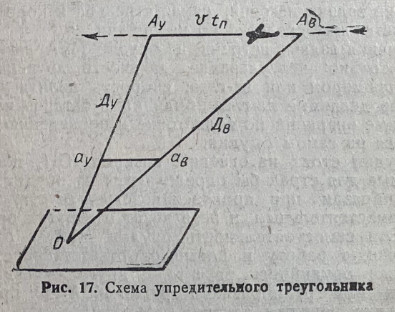
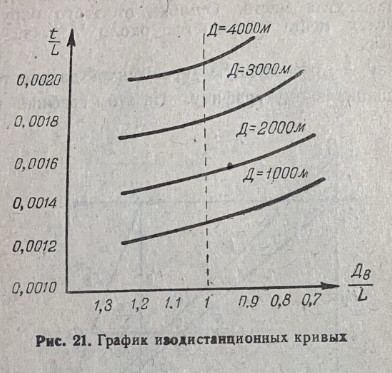
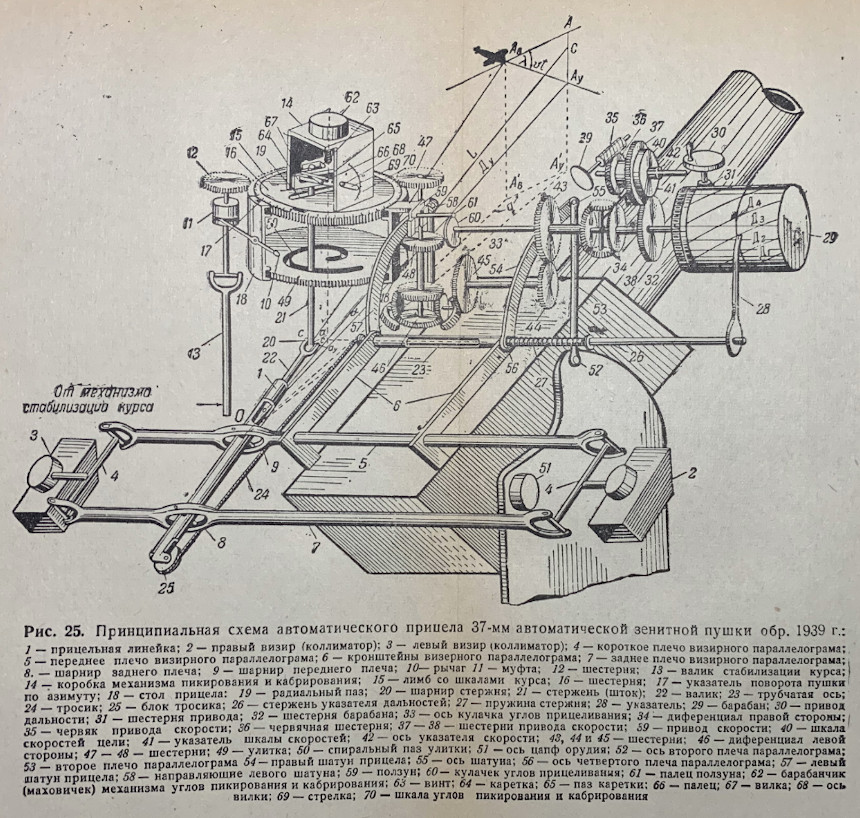
Труд от Вада.
Разбивка и прочее оригинальные.
Спасибо Ваду за проведенный большой объем теоретической работы, экспериментов и анализа.
==============================================================================
28 Сентябрь 2020 - 12:54
https://forum.il2stu...&comment=800245
Що?! Представитель кого бы говорил. ))
02 Ноябрь 2018 - 17:35
Хы... Не видать мне промокода халявного. )) Забанили меня окончательно. Когда, что...
Так что фиг им, а не обратная связь.


 Найти контент
Найти контент