3951 ответов в этой теме

[Dooplet_II]

https://www.youtube....i-mDGx5GEE&t=0s кто знает Таквью или как там оно называется,данные по перегрузу верно выводит?А то после такого ролика мне за синяков совсем страшно стало.

 Таквью напрямую из игры получает координаты ЦМ самолета. Значит, ускорения, как и скорости, легко и однозначно считаются. Вот с углами атаки и угловыми скоростями в ССК все более печально. Для точных значений Таквью не хватает данных из игры. 

[Vachik]

 Таквью напрямую из игры получает координаты ЦМ самолета. Значит, ускорения, как и скорости, легко и однозначно считаются. 

А вот фиг тебе:

https://forum.il2stu...&comment=716144

[Dooplet_II]

Про УА согласен. Про перегрузку... Вачик, координату Таквью из игры получает.100%. Как, зная изменение координаты, получить скорость и ускорение, знает десятиклассник. Так что заява Петровича про "похоже неправильно" не более, чем неуклюжая попытка отмазаться. " Вы считаете неправильно". Найди тот пост Петровича, когда он про тензоры птсал Кузнечику.

Сообщение изменено: Dooplet_II, 23 Август 2019 - 05:50.

[Starik]

Там уже охота на ведьм началась. Судорожно придумывают жесткий аргумент с обвинениями, а потом … ну в общем, вы знаете. 

[Dooplet_II]

Как только Петровича прижимают к стенке фактами, сначала следует про " не так меряете", а потом "Вы меня обижаете, идите на... в баню". Странно, что пока за видео с обстрелом бомберов никого не покарали. ))))

 Можно спросить у Петровича, что, по его мнению, Таквью считает правильно в БзХ, раз они его официально в конфигуратор игры встроили. Хотя,  такой вопрос в данный момент явно потянет на "вышку". 

Сообщение изменено: Dooplet_II, 23 Август 2019 - 10:49.

[Vachik]

Можно спросить у Петровича, что, по его мнению, Таквью считает правильно в БзХ, раз они его официально в конфигуратор игры встроили. 

Пока Петрович там сам себя хвалит да баны раздает, Вачик чуть-чуть провел тестов.

 

Сначала впал в ступор, ибо ну ни как такого не может быть. 

Рисовать самолетами синусы я не умею. Но раз десять одно и тоже. Чесал, чесал репу, пока не додумался сменить карту Сталинград на Лапино. Бинго. Сразу всё наладилось. Сколько нам открытий чудных...

 

Вираж 1.

Скорость 400 км/ч.

По вычислениям:

Крен 69.5^о

Перегрузка 2.83 G

В Таквью:

 

Вираж 2.

Скорость 283 км/ч.

По вычислениям:

Крен 69^о

Перегрузка 2.75 G

В Таквью:

 

Сколь нибудь значимых расхождений не вижу.

 

А знает ли Петрович? Да всё он знает. Просто очень не любит неудобных вопросов. По углу помнишь? Сразу радостно выскочил с разоблачением. А тут типа... спросите у лифшица. 

[Starik]

В 100500 раз попросили показометр перегрузок в игре сделать. 

Это ж новая проблема, если делать показометр, то как его научить косяки прятать.  Короче, "Чапай" думает. 

[Vachik]

Да видел я уже его ответ. Апосля своего поста. Это не даем, это не даем, это не даем... А что даем? Название миссии и даты, где проходила запись? Храбрые, ничего не боятся.

[Starik]

Лично мне уже давно понятно, для чего усталость лепят.

Ну не может Петрович сделать так, что бы его АФМ самолетов не позволяла летать им как пенопластовым, ну недотягивает он. По эффективности рулевых поверхностей на различных режимах недоделок уйма, в разрез ТТХ и прочей аэродинамике, допуски просто недопустимые. ) Решил, что усталостью пенопластовость сможет убрать …, а вдруг поможет хоть как-то. )))  

Но что будет мерилом? Усилия на ручке, так Dooplet ещё хрен знает когда табличку создал, где всё наглядно, особых преимуществ не наблюдается. А многолетнее издевательство ремнями, без возможности видеть прицел, как бы намекает, что это некультурные и бесчестные ребятишки. А значит, вместо того, чтобы вгонять самолеты в референс, Петрович в носу ковырялся.

Ну посмотрим, что наковырял. Не поиграем, так хоть поплюёмся.     

Сообщение изменено: Starik, 23 Август 2019 - 18:58.

[COBA]

А значит, вместо того, чтобы вгонять самолеты в референс, Петрович в носу ковырялся.

 

https://forum.il2stu...&comment=716266

каков будет ответ? 

[Starik]

Он уже там есть (ответ), ничего неожиданного, просто умное лицо.

Скоро ещё активно/пассивный подтянется. 

Сообщение изменено: Starik, 23 Август 2019 - 21:18.

[COBA]

Это пять!
https://forum.il2stu...&comment=716314

[Starik]

Да, активно/пассивный подтянулся. 

И как лихо разводят, один советует:

 

Мы (в отличие от DCS) не выдаём в TacView ни скорость, ни угол атаки, ни перегрузку. TacView это всё считает сам. Эти параметры действительно можно рассчитать обратным дифференцированием, зная координаты и угловое положение объекта, и используя  уравнения теоретической механики. Но каким именно способом этот расчёт реализован в TacView и почему он даёт совершенно явную, и такую большую статическую ошибку, я ответить не могу, это нужно спрашивать у разработчиков TacView.

И тут же некто верещит:

 

Вот она, попытка решить задачу чужими руками)))) Уже к разработчику таквью обратились )))

На мой взгляд, не очень адекватно всё это как-то. 

Жалкое зрелище, короче. 

[Vachik]

На мой взгляд, не очень адекватно всё это как-то. 

Жалкое зрелище, короче. 

Да как бы сложно назвать адекватностью ситуацию, когда тебя посылают к разработчику программы, ты идешь, приносишь ответ и ты же еще и дурак. )) И при этом, я так понимаю, надо верить Петровичу и только ему. ))))))

 

И девки пляшут интересно. Нигде нет таких тайн мадридского двора. И только у Петровича секреты секретные, простых смертных в смущение вводящие. 

[Dooplet_II]

Игра выдает изменение координат. Петрович предлагает по ним правильно посчитать ускорение( перегрузку). Разработчик Таквью не знает , как это правильно сделать и считает "не корректно"? Смешно. Как же тогда ему ума хватило эту прогу написать? Некорректно выдать ускорение в Таквью клиента можно только в одном случае: если игра Петровича некорректно выдает для клиента изменение координат обсчитываемого объекта.По причине кучи разных сетевых и читерских причин. Или по причине устарелости движка. Кто виноват? Петрович утверждает, что Таквью.
А самое интересное, что это ускорение у Петровича в игре уже считается и служит фундаментом для всей рисуемой картины. Таквью считает неправильно? Покажи "правильное" из игры, раз оно востребовано. Зачем этот садизм заставлять лириков самим считать физику? Откуда такая нелюбовь к своей аудитории и стремление показать, что она, дура, без семи потов нос себе не почешет, пока Петрович не разрешит?

[COBA]

Всем китам правильно считает, а селедке Петровича не правильно! Аууу Петрович, у вас все дома???)))

[Vachik]

... Некорректно выдать ускорение в Таквью клиента можно только в одном случае: если игра Петровича некорректно выдает для клиента изменение координат обсчитываемого объекта....

Я таки озадачился феноменом "синусоиды" получаемой на сталинградской карте. Сделал копии маневров на осенних картах Москва, Сталинград, Кубань и Лапино. До кучи сталинградскую карту зима и лето. На всех картах кроме сталинградских, рисуется правильно (примеры скринов см. выше). Отсюда вопрос: почему программа получая данные одного и того же формата, выдает такие разные результаты? В одном случае нормальные, в другом сплошной артефакт. Алгоритмы расчетов вдруг избирательно ломаются? Позвольте в это не верить. Как и словам Петровича. А верить разработчику Таквью, заявившему, что игра может отдавать некорректные/ошибочные данные.

 

Петрович гений. Он даже на ровном месте умеет создавать им же раздуваемые напряженности мирового масштаба, идущие только на пользу имиджа его же продукта. 

[Starik]

Программа, работающая во всех играх корректно, вдруг оказывается не правильной программой только для одной игры? 

Это насколько криво игра сделана, что стандартная телеметрия не работает.

И по какой-то мутной, даже очень мутной причине эта игра не имеет своей телеметрии, доступной пользователям.

Петрович, с "умным лицом" уже явный перебор. Я понимаю, что тебе пофиг на всех, но карма-то засирается.   

Сообщение изменено: Starik, 24 Август 2019 - 15:51.

[Vachik]

И по какой-то мутной, даже очень мутной причине эта игра не имеет своей телеметрии, доступной пользователям.

Ну почему же мутной? Всё таки очень прозрачно. Вот и подтверждение:

https://forum.il2stu...&comment=716427

Петрович панически боится. Чего боится, непонятно абсолютно. Ибо и у других, ошибок, несостыковок и прочей хрени в достатке. Но паникует лишь Петрович. Очевидно пунктик.

 

А вот человек ситуацию понимающий:

https://forum.il2stu...&comment=716380

И если разработчик не улавливает сути происходящего, то это плохой разработчик. Не компетентный. Не в расчетах. Нет. А именно, как разработчик игры.

============================================================================================================================

 

Петровичу.

Петрович! Лайкать посты, так или иначе тебя поддерживающие, считается моветоном даже для обычных форумчан. А уж для одного из главных, да еще и разработчика... У тебя совсем нет к себе уважения?

[Starik]

Ну мы же знаем, что если боится, значит есть чего.  А вот если боится панически то, вероятно, там уже не только рыло в пуху. 

[Vachik]

 А вот если боится панически то, вероятно, там уже не только рыло в пуху. 

Так нет же. Он еще в двенадцатом году уже на стреме был. Петрович сам этот пост вспомнил.

Да ладно, фиг с ним, с Петровичем. Но логично же было предположить, что заполучив "физиологию" и еще в довесок "накапливаемую не толерантность", игроки в части своей, зададутся вопросом - слющай, ничего не сделяль, только вощель... и тут вазой по башке. Будут ковырять величины перегрузок? Будут. А кроме, как в Таквью их взять негде, ибо Петрович в игре "правдивый" акселерометр не дал. Ну и не сложно предположить развитие спектакля. И в том что сейчас там развернулось, виноват никто иной, как сам Петрович. Может быть как инженер железок он и ничего, но как инженер человеческих душ, полный ноль. 

[Dooplet_II]

Так нет же. Он еще в двенадцатом году уже на стреме был. Петрович сам этот пост вспомнил.
Да ладно, фиг с ним, с Петровичем. Но логично же было предположить, что заполучив "физиологию" и еще в довесок "накапливаемую не толерантность", игроки в части своей, зададутся вопросом - слющай, ничего не сделяль, только вощель... и тут вазой по башке. Будут ковырять величины перегрузок? Будут. А кроме, как в Таквью их взять негде, ибо Петрович в игре "правдивый" акселерометр не дал. Ну и не сложно предположить развитие спектакля. И в том что сейчас там развернулось, виноват никто иной, как сам Петрович. Может быть как инженер железок он и ничего, но как инженер человеческих душ, полный ноль.

В подтверждение:
https://forum.il2stu...&comment=716460

[Starik]

И в том что сейчас там развернулось, виноват никто иной, как сам Петрович.

Наверное, пытается привлечь внимание. 

Там интересная мысль прозвучала "сначала надо попробовать, а потом обсуждать". Молодежь подтягивается? Которая не в курсе, что потом будет: "а что ж вы раньше-то молчали, переделывать не в приоритете". А потом по кругу - свои косяки бесплатно не устраняем!    

[Vachik]

https://forum.il2stu...&comment=716510

Ну да. Немножечко в очередной раз наи...ли.

И 70$ за Про версию, ни фига не копейки. Оно то конечно, некоторые ушлые скооперировались и купили ключи оптом, что снизило цену. Но всё равно, абыдно, да? )) 

[Starik]

Kirill, куда тебя понесло?! Какая мышечная усталость в этой игре?! Тебе ремней мало в красных самолетах, без прицела и хоть какого-то обзора сколько лет сидели, в смысле, мясом были!!! До сих пор эти ремни душат.

Хотя, это ж боль истребителей. 

Сообщение изменено: Starik, 25 Август 2019 - 18:28.

[Dooplet_II]

Тут Петрович прошелся по Таквью. Типа "не корректно" считает. И что это "инструмент веры". Но ведь можно заменить одну аббревиатуру другой без потери смысла и правоты высказывания:

https://cloud.mail.r.../2yMd/5cJpBxdoZ

Поэтому хотелось бы разобраться с "верю/не верю". На самом деле, все на уровне школьной физики ( конечно, не времен ЕГЭ, а еще советских стандартов).

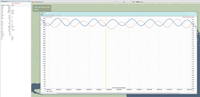
Итак, что выдает в Таквью игра? Смотрим:

https://cloud.mail.r.../3DC6/3Y9YcgzAn

Время , географические координаты в градусах до тринадцатого знака после запятой, высоту в метрах и углы :

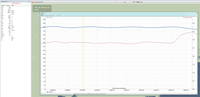
Прямо скажем, для расчета параметров  полета небогато. С какой частотой игра выдает эти данные не ясно, но в Таквью их можно посмотреть с дискретной периодичностью 0,1-0,11с. Что и как из всего этого можно посчитать?

   Изменение значений географических координат дает перемещение объекта за период между двумя выгрузками данных из игры. Перемещение,естественно , в градусах. Чтобы перевести их в метры, изменение широты умножаем на 111000м , и получаем изменение положения по широте в метрах, изменение долготы умножаем на 111000м и на косинус широты,- получаем изменение долготы. Если извлечь корень квадратный из суммы этих величин, мы получим перемещение объекта в проекции на горизонтальную плоскость Sгор. Если извлечем корень квадратный из суммы квадратов изменения высоты h и Sгор, получим перемещение объекта S за дискрету времени t между двумя выгрузками данных о параметрах движения объекта. Поделив S на t, получим значение средней скорости V на данном отрезке траектории. Чем меньше отрезок времени между выгрузками, тем ближе полученное значение к текущему истинному значению скорости. 

Теперь углы. Изменение значений углов, деленное на t, дает три значения средних угловых скоростей. Как определить ускорения? Если принять, что объект движется по радиусу, то:

               aц гор=Vгор^2/R=w^2*R 

отсюда среднее значение радиуса движения объекта за время t будет :

              R= Корень( (Sгор/t)^2/w^2), где w - это изменение курса в радианах, деленное на время t. 

           Зная R, найдем центробежное ускорение:

              aц гор= (Sгор/t)^2/R 

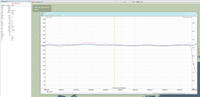
           Проделав те же операции для вертикальной скорости, изменения значения угла "Pitch", получим вертикальную составляющую ускорения ац вер.

            

           Корень из суммы квадратов этих ускорений даст модуль среднего ускорения a объекта  на участке траектории за время t. Известная величина угла крена дает возможность посчитать среднюю нормальную перегрузку, умножив a на косинус угла крена. 

          Так считает Таквью по данным из игры. А теперь самое  интересное. Почему "не корректно"? Потому что мы везде получаем "среднее". Да, чем меньше значение t, тем мы ближе придвигаем "среднее" к "корректному". Но ведь не Таквью задает t, а игра. Есть еще момент. Если за время t происходит смена знака изменения угла или перемещения, то значения средних скоростей (угловых и линейных) тоже становится некорректным. Но это тоже не вина Таквью. Чем криволинейнее траектория, тем больше "некорректность". Чем меньше значение t, через которое транслируются значения координат и углов, тем "некорректность" расчета Таквью меньше.  Петрович в расчете динамики объекта идет от силы через ускорение к пути. Но выдавая параметры для Таквью в виде пути (координат), он заведомо закладывает то, что Таквью посчитает ускорения и перегрузки "некорректно". Выдай Петрович для Таквью кроме координат и углов еще и угловые и линейные ускорения, то тактическая картинка в Таквью со 100% точностью отображала бы динамические параметры объектов. Но Петрович эти ускорения не дает. Почему?:

"А не даём мы дополнительную информацию для анализа ФМ в широкий доступ потому, чтобы не набежали "специалисты" (которые себя таковыми считают, хотя не могут решить элементарную задачу - вроде расчёта УА и перегрузки по треку TacView), и не накидали на вентилятор форум своих "экспертных" мнений, но уже с цифрами в руках. Нам итак еле хватает сил отбиваться от таких "специалистов" и без дополнительных реверансов в их сторону и подаренных им лишних поводов к чему бы ещё придраться."

[ROSS_Pups]

А с какой периодичностью данные отправляет дкс?

[Dooplet_II]

Не знаю. Но ДКС отправляет значения перегрузки. Поэтому, не так принципиально.

[jimmy_l]

Не знаю. Но ДКС отправляет значения перегрузки. Поэтому, не так принципиально.

Ну ты читал же его перлы про "амулетик".Вот это есть "амулетик",только для него.И им он будет отмахиваться, ссылаясь на некомпетентность создателя программы и проклятых хейтеров,а адвокаты будут требовать "просвещения в серые массы"))

Сообщение изменено: jimmy_l, 27 Август 2019 - 22:13.

[Vachik]

Так считает Таквью по данным из игры. А теперь самое  интересное. Почему "не корректно"? Потому что мы везде получаем "среднее". Да, чем меньше значение t, тем мы ближе придвигаем "среднее" к "корректному". Но ведь не Таквью задает t, а игра. 

Дуплет, спасибо за развернутый отлуп недобросовестному разработчику.

 

И я бы добавил. Не просто "среднее", а случайно "среднее". В игре есть собственный таймер по которому она и живет. Соответственно и у сервака тоже. SPS. А он под нагрузкой гуляет.  В добавок, насколько помню, Хан говорил, что положение другого самолета передается с некой аппроксимацией. То бишь, где-то примерно там. Пакетики потерялись, пакетики доставились, произошла поправка и тд и тп. Ну и что там получает Таквью? На деревню дедушке он получает. Что Петровичу и надо. Что Петрович и сделал. Потому и врет безбожно и выкручивается. И собственноручно расписывается в собственных страхах и неуверенностях. Увы ему, увы...

[COBA]

Погодите, щас окажется что Дуплет не правильно посчитал. Ну сопсна как всегда

[Dooplet_II]

Дуплет, спасибо за развернутый отлуп недобросовестному разработчику.

И я бы добавил. Не просто "среднее", а случайно "среднее". В игре есть собственный таймер по которому она и живет. Соответственно и у сервака тоже. SPS. А он под нагрузкой гуляет. В добавок, насколько помню, Хан говорил, что положение другого самолета передается с некой аппроксимацией. То бишь, где-то примерно там. Пакетики потерялись, пакетики доставились, произошла поправка и тд и тп. Ну и что там получает Таквью? На деревню дедушке он получает. Что Петровичу и надо. Что Петрович и сделал. Потому и врет безбожно и выкручивается. И собственноручно расписывается в собственных страхах и неуверенностях. Увы ему, увы...

Да я уж не стал про потери пакетов и аппроксимации координат.

Погодите, щас окажется что Дуплет не правильно посчитал. Ну сопсна как всегда

Ошибаться могут все. Я тоже. Может и разработчик Таквью ошибаться.

https://forum.il2stu...&comment=717095
Может, разработчик Таквью косинус широты забыл. Поправимо.
Но суть проблемы не изменится. Кто-то ошибается и не боится,"получив отлуп", исправиться и стать умнее, а кто-то:
"А не даём мы дополнительную информацию для анализа ФМ в широкий доступ потому, чтобы не набежали "специалисты" (которые себя таковыми считают, хотя не могут решить элементарную задачу - вроде расчёта УА и перегрузки по треку TacView), и не накидали на вентилятор форум своих "экспертных" мнений, но уже с цифрами в руках. Нам итак еле хватает сил отбиваться от таких "специалистов" и без дополнительных реверансов в их сторону и подаренных им лишних поводов к чему бы ещё придраться."

, - опасается сильно обнаружения ошибок, ибо придется отбиваться(отбиваться, не исправлять!).

Сообщение изменено: Dooplet_II, 28 Август 2019 - 06:42.

[COBA]

Ошибаться могут все. Я тоже. Может и разработчик Таквью ошибаться.
 

Саш, да я не про тебя писал 

а про гения, ведь только у него всё ПРАВИЛЬНО и ВЕРНО

[Dooplet_II]

Саш, да я не про тебя писал 

а про гения, ведь только у него всё ПРАВИЛЬНО и ВЕРНО

 

https://cloud.mail.r.../2yMd/5cJpBxdoZ

 

 Для большинства это вопрос религии. Но в отношении симуляторов Петрович сделал меня агностиком. 

[COBA]

https://cloud.mail.r.../2yMd/5cJpBxdoZ

Для большинства это вопрос религии. Но в отношении симуляторов

Таки да

[Starik]

Петрович сделал меня агностиком. 

То есть считаешь, что полученный Петровичем в процессе познания опыт, был неизбежно искажен его сознанием? А значит, Петрович принципиально не способен постичь точную и полную картину познанного? И косячит он в полной уверенности, что он истина в последней инстанции? Он не увиноват … 

Это его мощно отмазывает. 

Сообщение изменено: Starik, 28 Август 2019 - 12:13.

[ROSS_Pups]

Простите, что-то много газов , можно я спичкой чиркну?

31-е мая 2013 года

Будет ли модель полета в БзС учитывать явление сжимаемости воздуха, чтобы избежать проблем из "1946", где определенные самолеты летали слишком быстро, а в некоторых случаях даже преодолевали звуковой барьер?

Да, в БЗС учитывается влияние числа Маха и явление сжимаемости воздуха на аэродинамические характеристики самолётов.

Сообщение изменено: ROSS_Pups, 29 Август 2019 - 10:37.

[Starik]

Да, в БЗС учитывается влияние числа Маха и явление сжимаемости воздуха на аэродинамические характеристики самолётов.

Ого какой раритетный чес ты окопал! 

Но я могу чего-то не знать.

Сообщение изменено: Starik, 29 Август 2019 - 17:02.

[geny]

Уважаемый  Дуплет, мне нравится Ваше желание докопаться до истины с формулами и расчётами, но в расчете перегрузки, Вы сильно всё усложнили.

1. Я думаю все расчеты в ИЛ-2 производятся в линейной системе координат, а географические (сферические) есть следствие их пересчёта , а не наоборот. (карты слишком малы чтобы учитывать кривизну земного шара). Т.е. градусы получают из метров а не наоборот. (но это не суть)
2. Вы двигались в правильном направлении пытаясь найти перемещение за дискрету времени. Но почему то смешали в кучу перемещение центра масс (ЦМ) (координаты х,у,Н ) и вращение относительно ЦМ  (roll,pitch,yaw) пытаясь вычислить какие то радиусы и.т.д.

 

Всё гораздо проще:  

Вектор ускорения  ЦМ (он же перегрузка) определяется из координат и времени.

А roll,pitch,yaw позволяют «разложить» его (Вектор ускорения ЦМ(он же перегрузка)) по продольной, поперечной и вертикальной осям самолёта(составляющей).

(если уж совсем быть педантичным, и рассматривать перегрузки пилота , то да, угловое вращение по roll,pitch,yaw надо учитывать, поскольку пилот не находится в ЦМ, но мы говорим о самолете и его перегрузках, и здесь перегрузка  определяется движением ЦМ)

 

Предложу Вам несложный способ посчитать перегрузку по координатам и времени (см. ссылку).

 

https://cloud.mail.r.../2TdH/4CGCZiyQC

 

В примере моделируется движение  объекта в горизонтальной плоскости  с постоянной скоростью 100м/с по четверти окружности с радиусом 300м. с последующим переходом в прямолинейное.

1. Здесь можно  увидеть разницу между точным ускорением (перегрузкой) и расчётным.  
2. Изменив шаг дискретизации времени можно оценить  его влияние на погрешность расчёта.
3. Внеся время и координаты  (х,у) пресловутой фоки  из  ТакВью ( или еще откуда) можно с большой точностью, определить перегрузку , поскольку она маневрировала в горизонтали.
4. Добавив в расчёты  третью координату (высота) можно получить  «точное»(с ошибкой дискретизации) значение вектора ускорения (и вектора скорости) в трехмерном пространстве, а так же углы, образуемые вектором ускорения(и скорости) с координатными осями. (все формулы есть в инете)
5. Добавив roll,pitch,yaw получим ускорение по осям самолёта, а так же углы атаки . скольжения ,рысканья.
6. «Проинтегрировав» roll,pitch,yaw по времени поручим угловые скорости вращения.
7. …

… и так, мы получим «инструмент анализа», который никак не дают разработчики.

Я думаю, Дуплет сможет это сделать, если захочет.

С уважением!

P.S.  я не претендую на истину в последней инстанции, не исключаю ошибок  и всегда готов к конструктивному диалогу.

[=UA=TORT]

Сжимаемость же вроде относительно недавно сделали. А тут ещё 2013г......